Chỉ số Gini về phân phối thu nhập: 

Nếu f(x) là phương trình của đường còng Lorenz thì chỉ số Gini được cho bởi công thức: 

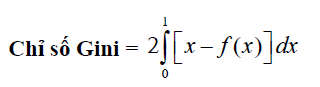
Chỉ số Gini luôn nằm giữa 0 và 1. 

- Chú ý: Chỉ số Gini bằng 0 thể hiện đường bình đẳng tuyệt đối - tức là tất cả mọi người đều có thu nhập bằng nhau. Chỉ số Gini bằng 1 thể hiện đường bất bình đẳng tuyệt đối - tức là một người nhận được tất cả các thu nhập và số còn lại không có thu nhập.

- Chỉ số Gini càng gần về 0, thì phân phối thu nhập càng bình đẳng. Chỉ số Gini càng gần về 1, thì thu nhập chỉ tập trung ở một số ít gia đình, khi đó phân phối thu nhập càng bất bình đẳng. Chỉ số Gini về phân phối thu nhập được sử dụng để so sánh phân phối thu nhập ở các thời điểm khác nhau, giữa các nhóm người khác nhau, trước và sau khi đánh thuế và trong các trường hợp khác nhau.

Vi dụ: Đường cong Lorenz biểu diễn phân phối thu nhập của một quốc gia trong năm 2015 được cho bởi f(x) = x^2.6. Các nhà kinh tế dự đoán rằng đường cong Lorenz của quốc gia đó năm 2025 sẽ là g(x) = x^1.8. Tính chỉ số Gini về phân phối thu nhập của mỗi đường cong và giải thích kết quả thu được ?

Áp dụng công thức trên: Ta có: 

- Chỉ số Gini vào năm 2015 là: 

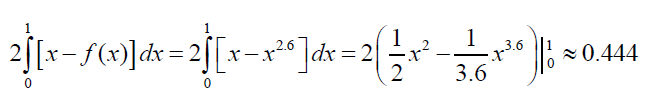
- Chỉ số Gini vào năm 2025 là: 

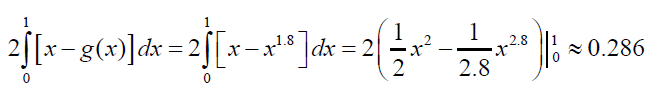
Nếu dự đoán của các nhà kinh tế là chính xác thì chỉ số Gini sẽ giảm dần, điều này có nghĩa là phân phối thu nhập trong năm 2025 sẽ bình đẳng hơn so với năm 2015.