Ứng dụng của phương trình vi phân tách biến trong việc giải bài toán nhiệt độ phòng (theo định luật làm mát của Newton)
Sưởi ấm một tòa nhà văn phòng (Định luật làm mát của Newton)
Bài toán đặt ra: Giả sử vào mùa đông nhiệt độ ban ngày trong một tòa nhà văn phòng nào đó được duy trì ở mức 70°F. Hệ thống sưởi tắt lúc 10 giờ tối và bật lại lúc 6 giờ sáng. Vào một ngày nào đó, nhiệt độ bên trong tòa nhà lúc 2 giờ sáng được xác định là 65°F. Nhiệt độ bên ngoài là 50°F lúc 10 giờ tối và giảm xuống 40°F lúc 6 giờ sáng. Nhiệt độ bên trong tòa nhà khi bật máy sưởi lúc 6 giờ sáng là bao nhiêu?
Thông tin vật lý: Các thí nghiệm cho thấy rằng tốc độ thay đổi theo thời gian của nhiệt độ T của vật B (vật dẫn nhiệt tốt, chẳng hạn như quả cầu đồng) tỷ lệ thuận với độ chênh lệch giữa T và nhiệt độ của môi trường xung quanh (định luật làm mát của Newton).
Hướng giải quyết:
Bước 1. Thiết lập mô hình. Gọi T(t) là nhiệt độ bên trong tòa nhà và $T_{A}$ nhiệt độ bên ngoài (được coi là không đổi theo định luật Newton). Khi đó theo định luật Newton, ta có
\(\frac{{dT}}{{dt}} = k\left( {T - {T_A}} \right)\;\left( * \right)\)
Những quy luật thực nghiệm như vậy được rút ra từ những giả định lý tưởng hóa hiếm khi đúng. Tuy nhiên, ngay cả khi một mô hình có vẻ không phù hợp lắm với thực tế (như trong trường hợp hiện tại), nó vẫn có thể cung cấp thông tin định tính có giá trị. Để xem mô hình tốt đến đâu, kỹ sư sẽ thu thập dữ liệu thực nghiệm và so sánh với tính toán từ mô hình.
Bước 2. Giải pháp chung. Chúng tôi không thể giải (*) vì chúng tôi không biết $T_{A}$, chỉ biết nó dao động trong khoảng từ 40°F đến 50°F, vì vậy chúng tôi tuân theo Quy tắc Vàng: Nếu bạn không thể giải quyết vấn đề của mình, hãy thử giải một vấn đề đơn giản hơn. Chúng ta giải (*) bằng hàm chưa biết $T_{A}$ được thay thế bằng giá trị trung bình của hai giá trị đã biết tức là 45°F. Vì lý do vật lý, chúng ta có thể kỳ vọng rằng điều này sẽ cho chúng ta một giá trị gần đúng hợp lý của T trong tòa nhà lúc 6 giờ sáng. Đối với hằng số (hoặc bất kỳ giá trị không đổi nào khác), phương trình vi phân (*) có thể tách biến.
\(\frac{{dT}}{{T - 45}} = kdt \to \ln \left| {T - 45} \right| = kt + {c^*} \to T\left( t \right) = 45 + c{e^{kt}}\;\;\left( {c = {e^{{c^*}}}} \right)\)
Bước 3. Giải pháp cụ thể. Chúng ta chọn 10 P.M ứng với $t = 0$. Khi đó điều kiện ban đầu đã cho là $T(0) = 70$ và mang lại một nghiệm cụ thể, gọi nó là $T_p$. Bằng cách thay thế,
\(T\left( 0 \right) = 45 + c{e^0} \to c = 25 \to {T_p}\left( t \right) = 45 + 25{e^{kt}}\)
Bước 4. Xác định k. Chúng ta sử dụng thười điểm lúc 2 A.M tức là ứng với $t = 4$. Giải đại số tìm k và chèn k vào sẽ được
\({T_p}\left( 4 \right) = 45 + 25{e^{4k}} = 65 \to {e^{4k}} = 0.8 \to k = \frac{1}{4}\ln 0.8 = - 0.056 \to {T_p}\left( t \right) = 45 + 25{e^{ - 0.056t}}\)
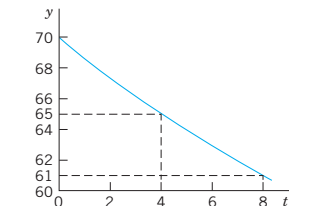
Bước 5. Trả lời và giải thích. Lúc 6 giờ sáng (ứng với $t = 8$) ta có
\({T_p}\left( 8 \right) = 45 + 25{e^{ - 0.056 \cdot 8}} = 61{(^0}F)\)
Do đó nhiệt độ trong tòa nhà giảm 9°F, một kết quả có vẻ hợp lý.
Bài viết liên quan


