Ứng dụng của phân phối chuẩn

              Đường cong phân phối chuẩn tắc có thể được sử dụng để giải quyết một loạt các vấn đề thực tế. Yêu cầu duy nhất là biến phải tuân theo phân phối chuẩn hoặc tiệm cận phân phối chuẩn. Một số bài toán kiểm định toán học đặt ra là xác định liệu một biến có được phân phối chuẩn hay không. Đối với tất cả các vấn đề được trình bày trong chương này, các biến được giả định là phân phối chuẩn hoặc tiệm cận phân phối chuẩn.

Để giải quyết các vấn đề bằng cách sử dụng phân phối chuẩn tắc thì ta biến đổi biến ban đầu thành một biến phân bố chuẩn hóa bằng cách sử dụng công thức:

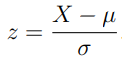
Đây là công thức để chuyển đổi một biến bất kì thành biến có phân phối chuẩn. Chẳng hạn, giả sử điểm số của một bài kiểm tra chuẩn.

 Ví dụ một cuộc điều tra của Liên đoàn bán lẻ Quốc gia cho thấy phụ nữ chi trung bình 146, 21 đô la cho những ngày lễ Giáng sinh. Giả sử độ lệch chuẩn là 29, 44 đô la. Để tìm số phần trăm phụ nữ chi tiêu dưới 160 đô la biết biến có phân phối chuẩn, ta sử dụng phân phối chuẩn để giải quyết vấn đề này như sau:

Bước 1: Vẽ hình và mô tả diện tích của bài toán như hình vẽ.

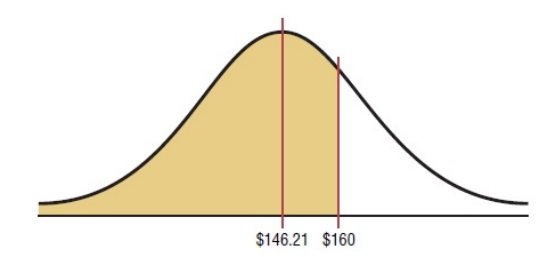
              Bước 2: Tìm giá trị z tương ứng với 160 đô la.

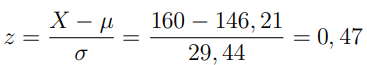
             Bước 3: Tìm diện tích bằng cách sử dụng bảng phụ lục ta có diện tích phần bên trái dưới đường phân phối z ứng với z = 0, 47 là 0, 6808.

              Vậy, có 0, 6808 hay 68, 08% số phụ nữ chi tiêu ít hơn 160 đo la vào mùa Giáng sinh.