Trong Lý thuyết đồ thị, tô màu đồ thị (tiếng Anh: graph coloring) là trường hợp đặc biệt của gán nhãn đồ thị, mà trong đó mỗi đỉnh hay mỗi cạnh hay mỗi miền của đồ thị có thể được gán bởi một màu hay một tập hợp các màu nào đó. Tô màu đồ thị có thể là:

• tô màu đỉnh (tiếng Anh: vertex coloring) là gán cho mỗi đỉnh của đồ thị một màu nào đó sao cho không có hai đỉnh nào liền kề lại trùng màu nhau;
• tô màu cạnh (tiếng Anh: edge coloring) là gán cho mỗi cạnh của đồ thị một màu nào đó sao cho sao cho không có 2 cạnh nào trùng màu;
• tô màu miền (tiếng Anh: face coloring) là gán cho mỗi miền của đồ thị phẳng một màu sao cho không có 2 miền có chung đường biên lại cùng màu.

Sắc số (tiếng Anh: chromatic number) của một đồ thị là số màu ít nhất để tô các đỉnh. Sắc số của đồ thị G được ký hiệu là χ(G).

Số màu cạnh (tiếng Anh: chromatic index) của một đồ thị là số màu ít nhất dùng để tô các cạnh. Số màu cạnh của đồ thị G được ký hiệu là χ'(G).

Số màu cạnh của đồ thị G bất kì bằng sắc số của đồ thị đường L((G)) của đồ thị đó:

χ'(G) = χ(L(G)),

do đó việc nghiên cứu tô màu cạnh của G tương đương với nghiên cứu tô màu đỉnh của L(G).

Các định lý và tính chất

Các giá trị giới hạn của sắc số

Rõ ràng sắc số của một đồ thị sẽ không vượt quá số đỉnh của nó (bậc của đồ thị):

1≤χ(G)≤n..

Nếu G có clique kích thước k thì cần ít nhất k màu để tô màu đỉnh cho clique này (xem thêm bài về đồ thị đầy đủ), như vậy sắc số của một đồ thị sẽ không nhỏ hơn chỉ số clique của đồ thị đó:

χ(G)≥ω(G).

Nếu đồ thị đơn G có bậc cực đại bằng Δ(G) thì sắc số của nó không vượt quá Δ(G)+1^[1].

hiện

Chứng minh

Tổng quát hơn là định lý Brook, định lý khẳng định rằng:

Tất cả mọi đồ thị đơn và liên thông G, ngoại trừ đồ thị đầy đủ Kn và đồ thị chu trình bậc lẻ Wn, đều có sắc số nhỏ hơn hoặc bằng bậc cực đại:

χ(G)≤ Δ(G).

Nếu đồ thị G có m cạnh thì sắc số của nó thỏa mãn:

χ(G)(χ(G)−1)≤2m.

hiện

Chứng minh

Một số định lý liên quan của sắc số

Định lý 1

Bất cứ chu trình độ dài lẻ nào cũng đều có sắc số bằng 3

Chứng minh: Giả sử chu trình có độ dài là 2n+1 ta chứng minh theo số n

• n=1 chu trình gồm 3 đỉnh mà 2 đỉnh bất kì đều kề nhau ⇒ dùng đúng 3 màu để tô
• (n)⇒(n+1) Giả sử α là một chu trình có độ dài 2(n+1)+1=2n+3 với các dãy đỉnh là x1, x2,...,x2n+1,x2n+2,x2n+3.

Nối x1 với x2n+1 ta được một chu trình α'có độ dài 2n+1.

Theo giả thuyết quy nạp chu trình α' có sắc số bằng 3.

Lấy màu của x1 tô cho x2n+2 còn màu của x2n+1 tô cho x2n+3.

Chu trình α được tô màu mà không thêm màu mới vào.

Vậy chu trình α có sắc số bằng 3

Định lý 2

Đồ thị đầy đủ n đỉnh K_n có sắc số bằng n

Một số tiêu chuẩn đơn giản để kiểm tra xem 1 đồ thị có hai sắc số hay không:

• Ta có định lý: Giả sử đồ thị G có ít nhất một cạnh. Đồ thị G có hai sắc số khi và chỉ khi G không có chu trình đơn vô hướng độ dài lẻ.

Chứng minh:

• Giả sử G là đồ thị có hai sắc số. Theo Định lý 1 thì G không thể có chu trình đơn vô hướng độ dài lẻ.
• Ngược lại giả sử G không có chu trình đơn vô hướng độ dài lẻ. Không mất tính tổng quát có thể xem G liên thông.

Chọn 1 đỉnh a nào đó bất kì trong đồ thị

Đặt m(a)=0 (m: số màu)

Với x ≠ a Ta ký hiệu d(x)là độ dài đường đi vô hướng ngắn nhất nối a vớix

Đặt m(x)=d(x) mod 2

Ta sẽ chứng minh m là hàm màu của G

Giả sử x,y kề nhau

Lấy d(x) là đường đi vô hướng ngắn nhất nối a với x có độ dài d(x)

d(y) là đường đi vô hướng ngắn nhất nối a với y có độ dài d(y)

Chu trình đơn [d(x),(x,y),d(y)] có độ dài d(x)+d(y)+1phải là một số chẵn

Vậy thì d(x)+d(y) là một số lẻ ⇒ d(x),d(y) khác nhau tính chẵn lẻ

⇒m(x) ≠ m(y)

Hàm tô màu m có hai giá trị, vậy sắc số ≤ 2. G có ít nhất một cạnh nên sắc số của nó bằng 2

Từ định lý trên ta có hệ quả sau: Tất cả các chu trình độ dài chẵn đều có sắc số bằng 2.

Định lý 3

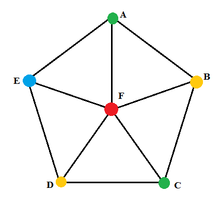
Phát biểu: Nếu G có chứa 1 đồ thị con đẳng cấu với K_n thì x(G)≥n.