Tính Xấp Xỉ Tích Phân
Có hai tình huống mà ta không thể tính chính xác giá trị của một tích phân xác định.
1. Tình huống đầu tiên là khi ta cần biết một nguyên hàm của một hàm số f để tính tích phân của hàm số đó trên đoạn [a,b] bằng cách sử dụng Định lý cơ bản của Giải tích. Tuy nhiên, đôi khi việc tìm một nguyên hàm là điều rất khó, thậm chí là không thể. Lấy ví dụ như ta không thể tính các tính phân sau đây một cách chính xác:
\(\int\limits_{0}^{1}{{{e}^{{{x}^{2}}}}dx}\), \(\int\limits_{-1}^{1}{\sqrt{1+{{x}^{3}}}dx}\).
2. Tình huống thứ hai là khi hàm số được xác định từ một thí nghiệm khoa học thông qua việc đọc thiết bị hoặc từ dữ liệu thu thập được. Như vậy, không có công thức nào dành cho hàm số dạng này.
Do đó ở cả hai trường hợp trên, ta cần tìm các giá trị xấp xỉ (gần đúng) của các tích phân xác định. Chúng ta cũng đã biết một số phương pháp như vậy. Ta đã biết tích phân được định nghĩa là giới hạn của các tổng Riemann. Vì vậy, bất kỳ tổng Riemann nào cũng có thể được sử dụng như một phép tính xấp xỉ của tích phân. Nếu chúng ta chia đoạn [a,b] thành n khoảng có độ dài bằng nhau là \(\Delta x=(b-a)/n\) . Có 2 cách tính xấp xỉ mà ta có thể sử dụng là Quy tắc trung điểm và Quy tắc hình thang:

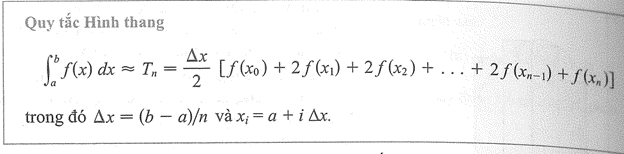
Bài viết liên quan
- Học Cách "Tư Duy Thuật Toán": Kỹ Năng Sinh Tồn Của Sinh Viên Trước Làn Sóng Tự Động Hóa 2026
- Sao Hỏa: Bản Giao Hưởng Của Sắt, Carbon Và Những Bí Ẩn Hóa Học
- Toán học: "Ngôn ngữ" đằng sau linh hồn của máy móc
- Dẫn xuất Halogen: Từ Nền Tảng Hóa Học Đến Ứng Dụng Trong Công Nghệ Thực Phẩm
- CÔNG NGHỆ THỊT THỰC VẬT


