Đối với những trường hợp không tìm được nguyên hàm, ta sử dụng tổng trái, tổng phải để xấp xỉ tích phân xác định của một hàm số và tính chính xác giá trị của tích phân xác định bằng các định lý tính toán cơ bản. Trong mục này, ta tiếp tục thảo luận một số phương pháp khác để xấp xỉ tích phân và quy trình tìm ra giá trị chính xác của tích phân xác định của một số hàm tiêu chuẩn. Xấp xỉ tích phân xác định bằng tổng trái và tổng phải là một phương pháp quan trọng nhưng ít hiệu quả. Ta cần lập nhiều hình chữ nhật, tính nhiều tổng để kết quả xấp xỉ gần đúng. Quy tắc hình thang và quy tắc Simpson sẽ cung cấp hai phương pháp xấp xỉ tốt hơn để tính được tích phân một cách chính xác.

Hình thang trong Hình 1- cho ta xấp xỉ về diện tích phần giữa đồ thị hàm f  và trục hoành- chính xác hơn

Hình 1

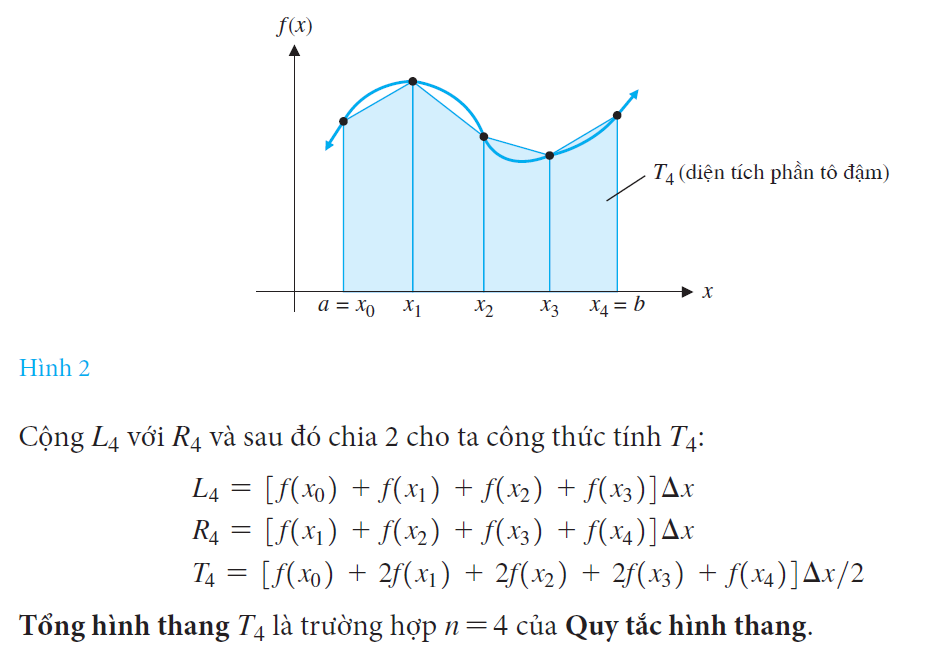
Lưu ý rằng diện tích hình thang trong Hình 1 [công thức (1)] là diện tích trung bình của hai diện tích hình chữ nhật trái và phải. Do đó, giá trị trung bình T4 của tổng trái L4 và tổng phải R4 đối với hàm số f trên đoạn [a, b] là tổng diện tích của 4 hình thang (Hình 2).