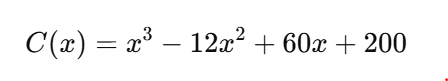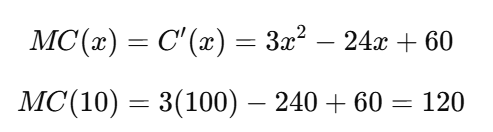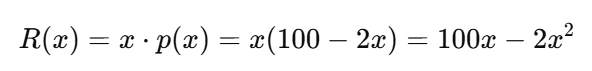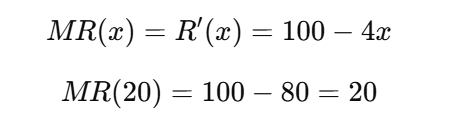1. Khái niệm cơ bản:

Trong kinh tế học vi mô, khi nghiên cứu quá trình sản xuất và tiêu thụ hàng hóa, ta thường quan tâm đến hai hàm số chính.

• Chi phí sản xuất C(x): là tổng chi phí để sản xuất x đơn vị sản phẩm (gồm chi phí cố định và chi phí biến đổi).

• Doanh thu R(x): là tổng doanh thu thu được khi bán x đơn vị sản phẩm (bằng giá bán nhân với số lượng).

1.1. Chi phí cận biên (Marginal Cost – MC)

       * Định nghĩa: Chi phí cận biên tại mức sản lượng x đvsp là phần chi phí tăng thêm để sản xuất thêm một đơn vị sản phẩm, ký hiệu MC(x).

• Về mặt toán học: MC(x)=C′(x)

Nghĩa là, chi phí cận biên là đạo hàm của hàm chi phí theo sản lượng.

1.2. Doanh thu cận biên (Marginal Revenue – MR)

        * Định nghĩa: Doanh thu cận biên tại mức sản lượng x là phần doanh thu tăng thêm khi bán thêm một đơn vị sản phẩm.

• Về mặt toán học:  MR(x)=R′(x)

Nghĩa là, doanh thu cận biên là đạo hàm của hàm doanh thu theo sản lượng.

Cả hai khái niệm đều là ứng dụng của đạo hàm trong giải tích, phản ánh tốc độ thay đổi tức thời của chi phí hoặc doanh thu theo số lượng sản phẩm.

2. Ý nghĩa kinh tế

• Nếu MC(x) < MR(x), tức là chi phí để sản xuất thêm 1 đơn vị nhỏ hơn doanh thu thu được từ đơn vị đó → sản xuất thêm có lợi nhuận.

• Nếu MC(x) > MR(x) → sản xuất thêm gây lỗ.

• Điểm cân bằng tối ưu thường đạt tại MC(x)=MR(x), tức sản lượng tối ưu.

3. Bài toán ứng dụng

Bài toán 1: Tính chi phí cận biên

Một công ty có hàm chi phí (nghìn đồng): 

trong đó x là số sản phẩm (đơn vị).

Yêu cầu: Tính chi phí cận biên tại x=10.

Lời giải:

→ Nghĩa là khi đang sản xuất 10 sản phẩm, chi phí để sản xuất thêm 1 sản phẩm nữa là 120 (nghìn đồng).

Bài toán 2: Tính doanh thu cận biên

Một công ty bán sản phẩm với hàm cầu (nghìn đồng/đơn vị):  p(x)=100−2x

trong đó p(x) là giá bán khi tiêu thụ x đơn vị.

Doanh thu:

Yêu cầu: Tính doanh thu cận biên khi x=20.

Lời giải:

→ Nghĩa là nếu đang bán 20 sản phẩm, doanh thu tăng thêm khi bán thêm 1 sản phẩm nữa là 20 (nghìn đồng).

Vậy, 

• Chi phí cận biên và doanh thu cận biên là công cụ toán học quan trọng trong kinh tế, giúp doanh nghiệp quyết định sản xuất bao nhiêu sản phẩm để tối đa hóa lợi nhuận.

• Chúng là ứng dụng trực tiếp của đạo hàm trong giải tích vào thực tiễn quản lý và sản xuất.