Như chúng ta đã biết, lý thuyết hệ phương trình tuyến tính giúp chúng ta giải quyết khá nhiều các bài toán trong kinh tế như bài toán cân bằng thị tường, bài toán tối ưu hoá trong sản xuất, bài toán cân đối liên ngành input - output. Leontief, ... 

   Thị trường cân bằng khi cung = cầu. Trong mô hình cân bằng thị trường, vấn đề chính là xác định giá trị các biến để chúng thoả mãn các điều kiện cân bằng. Như chúng ta xét mô hình xác định giá cả thị trường (ký hiệu là p) của một mặt hàng sao cho trong một đơn vị thời gian nào đó khối lượng hàm cung theo giá (ký hiệu Q_S)  bằng khối lượng hàm cầu theo giá ký hiệu là (Q_D). 

   Xét thị trường có ba mặt hàng sau đây: 

   Các nhà kinh tế nhận định rằng, hàm cung và hàm cầu của ba mặt hàng cua, ốc hương và tôm tại thị trường Đà Nẵng lần lượt như sau: 

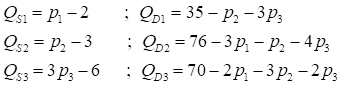
Trong đó p1, p2, p3  lần lượt là giá của mặt hàng cua, ốc hương và tôm. Hãy xác định giá cân bằng thị trường của ba mặt hàng trên?

Hướng dẫn giải: Thị trường cân bằng khi cung = cầu nên ta có hệ phương trình 

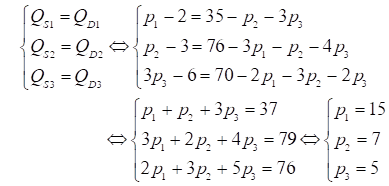
   Vậy giá cân bằng thị trường của mặt hàng trên là: (15, 7, 5)