Ứng dụng của xác suất trong đời sống

Bài viết này sẽ trình bày về một ứng dụng của xác suất thống kê trong đời sống chính là dùng xác suất để ước lượng tổng thể.

1. Đặt vấn đề

Như đã biết, phương pháp chính xác nhất để thống kê là điều tra đối với từng cá thể. Tuy nhiên việc làm này rất tốn kém và mất nhiều thời gian đối với các tổng thể lớn. Do đó, thông thường để có được số liệu về tổng thể lớn, phương pháp hay dùng là chỉ điều tra trong một mẫu nhỏ từ tổng thể, rồi từ đó sử dụng các lý thuyết của xác suất thống kê để đưa ra một kết luận (có độ chính xác tương đối) cho tổng thể lớn. Đấy là một trong các ứng dụng của xác suất thống kê trong ước lượng tổng thể.

2. Lý thuyết liên quan

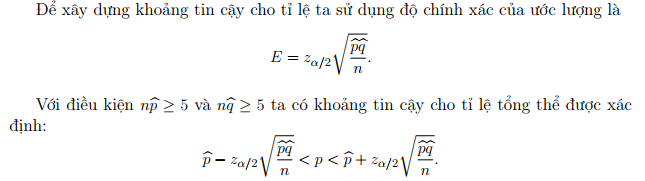
3. Một ví dụ thường gặp trong đời sống:

Đây là bài toán thường ngày của những người ngư dân nuôi cá. Sau khoảng thời gian nuôi cá, họ muốn biết xem số cá hiện có trong hồ của họ là bao nhiêu để có những kế hoạch nuôi đúng cách. Tuy nhiên, vấn đề đặt ra là chúng ta không thể bắt hết cá lên bờ, rồi sau đó đếm thủ công được vì làm như vậy sẽ ảnh hưởng không tốt đến cá cũng như không môi trường sống của chúng? Vậy cách làm của họ là như thế nào.

Ban đầu, bắt một lượng n cá trong hồ lên. Ở đây, giả sử n = 50. Đánh dấu chúng rồi thả lại vào hồ. Sau đó, bắt bất kì một lượng cá khác lên, rồi tính tỉ lệ p là tỉ lệ số cá được đánh dấu trong lần bắt này. Tỉ lệ p này dùng để xác định tỉ lệ p của tổng số cá được đánh dấu với số cá trong hồ.

Ví dụ bắt 20 con cá, trong đó thấy có 2 con được đánh dấu. Khi đó, p = 2/20 = 10%. Ước lượng tổng số cá trong hồ là n/p. Ở ví dụ vừa xét, ước lượng tổng số cá trong hồ là khoảng 50/10% = 500 con.