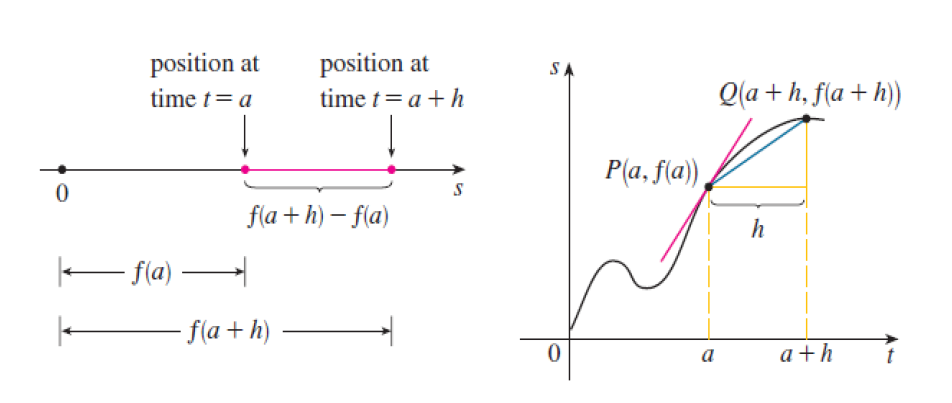
Bài toán mở đầu của đạo hàm
Trong các bài toán mở đầu phần giới hạn, ta đã đoán được giá trị độ dốc của tiếp tuyến và giá trị vận tốc của chuyển động, dựa trên cơ sở xét tỉ số. Bây giờ, ta đã định nghĩa giới hạn và có các kỹ thuật tính giới hạn. Chúng ta trở lại bài toán xác định tiếp tuyến và vận tốc cùng với tính độ dốc của tiếp tuyến, vận tốc và sự biến thiên theo tỷ lệ khác.
Cho đường cong C có phương trình y = f(x) và ta muốn tìm tiếp tuyến của C tại điểm (a, f(a)). Khi đó, ta xét các điểm gần Q(x, f(x)) trong đó x khác a và tính độ dốc của cát tuyến PQ.
mPQ= (f(x)-f(a))/(x-a)
Để Q gần P chạy theo đường cong C thì x phải tiến về a. Nếu mPQ tiến đến một con số m khi đó ta xác định tiếp tuyến t là đường thẳng qua P với hệ số góc m.
Bài viết liên quan
- Mặt trái của việc sinh viên lệ thuộc quá nhiều vào ChatGPT trong học tập môn Toán
- Chiến lược "Huấn luyện" Siêu Tảo: Từ Tiến hóa Tự nhiên đến Công nghệ Thương mại
- ỨNG DỤNG ĐỊNH LÝ ĐỊNH LÝ CHEBYSHEV
- PHƯƠNG PHÁP MẠ BĂNG TRONG CHẾ BIẾN SẢN PHẨM THỦY SẢN LẠNH ĐÔNG
- Học Cách "Tư Duy Thuật Toán": Kỹ Năng Sinh Tồn Của Sinh Viên Trước Làn Sóng Tự Động Hóa 2026

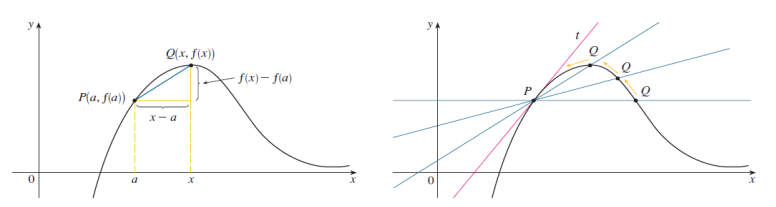
.PNG)