Áp dụng công thức tích phân xác định để tìm giá trị tương lai của dòng tiền liên tục
Ta biết công thức tính số dư khi lãi được tính liên tục là A = Pe^(rt).
Trong đó, P là số tiền gốc (hay giá trị hiện tại), A là số dư (hay giá trị tương lai), r là
lãi suất hằng năm của lãi kép liên tục (được biểu diễn dưới dạng số thập phân), và t
là thời gian tính theo năm.
Chẳng hạn, nếu lãi kép liên tục có lãi suất 12% thì giá trị tương lai của vốn đầu tư 10,000 đvtt sau 5 năm là A = 10,000e^(0.12x5) = 18,221 (đvtt).
Ta muốn áp dụng khái niệm giá trị tương lai vào việc tính thu nhập có được từ
dòng tiền liên tục. Giả sử f(t) là tốc độ lưu chuyển của dòng tiền liên tục và thu nhập
sinh ra từ dòng tiền liên tục này được đầu tư ngay khi nhận được với lãi suất liên tục
r. Ta đã biết cách tính tổng thu nhập nhận được sau T năm, nhưng làm thế nào để
tính được tổng lượng tiền và tiền lãi có được từ thu nhập này? Do lượng tiền được
nhận một cách liên tục, ta không thể áp dụng công thức A = Pe^(rt). Công thức này chỉ
có giá trị cho khoản tiền gốc P riêng lẻ, không phải đối với dòng tiền liên tục.
Ta sử dụng phương pháp tính gần đúng bằng tổng Riemann có thể áp dụng được công thức A = Pe^(rt). Trước hết, ta chia khoảng thời gian [0, T] thành n đoạn con bằng nhau và có độ dài là ∆t, chọn một điểm c_k tùy ý trên mỗi đoạn con. Khi đó, tổng thu nhập nhận được trong khoảng thời gian từ t = t_{k – 1} đến t = t_k bằng diện tích của phần dưới đồ thị f(t) trên đoạn đang xét và được xấp xỉ bằng f(c_k) ∆t. Thu nhập nhận được trong khoảng thời gian này sẽ cho tiền lãi trong khoảng xấp xỉ T – c_k năm. Vậy, từ công thức tính giá trị tương lai A = Pe^(rt) với P = f(c_k) ∆t và t = T – c_k, giá trị tương lai của lượng tiền sinh ra trong khoảng thời gian từ t = t_{k – 1} đến t = t_k được xấp xỉ bằng
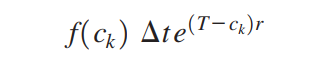
Khi đó, tổng các giá trị tương lai trên n đoạn con được xấp xỉ bằng
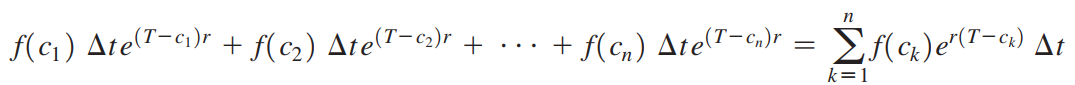
Phương trình trên có dạng của tổng Riemann, qua giới hạn lấy tích phân xác định
Do đó, giá trị tương lai, kí hiệu là FV, của thu nhập sinh ra từ dòng tiền liên tục được xác định bởi công thức
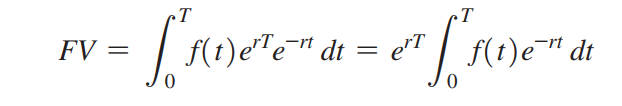
(Do r và T là những hằng số, ta có thể đưa e^(rT) ra ngoài dấu tích phân)
Cho tốc độ lưu chuyển của dòng tiền liên tục là f(t) = 5,000e^(0.04t) và lãi suất liên tục là 12%/năm. Khi đó, giá trị tương lai của dòng tiền sau 5 năm, được xác định bởi công thức
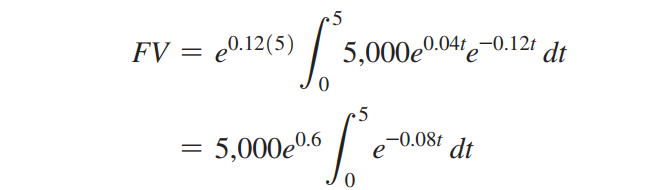
Tính kết quả ta được FV = 37,545 đvtt.
Bài viết liên quan


