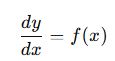LỊCH SỬ HÌNH THÀNH BÀI TOÁN GIẢI PHƯƠNG TRÌNH VI PHÂN CẤP MỘT

1. Mở đầu
Trong lịch sử toán học, nhiều khái niệm không ra đời từ nhu cầu thuần túy lý thuyết mà xuất phát từ việc mô tả các hiện tượng biến thiên trong tự nhiên. Phương trình vi phân cấp một là một ví dụ tiêu biểu. Việc giải các phương trình dạng này ban đầu gắn liền với khái niệm đạo hàm và tích phân, sau đó dần phát triển thành một lĩnh vực nghiên cứu độc lập.

2. Giai đoạn hình thành: từ đạo hàm đến phương trình vi phân
Vào thế kỷ XVII, khi Newton và Leibniz xây dựng phép vi phân và tích phân, đạo hàm được hiểu là tốc độ biến đổi tức thời của đại lượng. Từ các bài toán cơ học và thiên văn, những quan hệ dạng

xuất hiện một cách tự nhiên. Việc “giải” phương trình vi phân khi đó chỉ đơn giản là tìm hàm có đạo hàm cho trước, tức thực hiện phép tích phân. Đây là hình thức sơ khai của bài toán giải phương trình vi phân cấp một.

3. Sự mở rộng và hệ thống hóa trong thế kỷ XVIII
Sang cuối thế kỷ XVII và đầu thế kỷ XVIII, anh em nhà Bernoulli đã nghiên cứu nhiều lớp phương trình vi phân cấp một, đặc biệt là các phương trình tách biến và tuyến tính. Những bài toán nổi tiếng như đường đẳng thời cho thấy phương trình vi phân không chỉ là công cụ kỹ thuật, mà còn phản ánh các quy luật tối ưu trong tự nhiên.
Leonhard Euler tiếp tục hệ thống hóa các phương pháp giải, đưa ra cách phân loại rõ ràng và chuẩn hóa ký hiệu. Nhờ đó, phương trình vi phân cấp một được xem như một đối tượng nghiên cứu thống nhất trong giải tích.

4. Chuyển biến về mặt lý thuyết trong thế kỷ XIX
Đến thế kỷ XIX, cùng với sự phát triển của giải tích hiện đại, trọng tâm nghiên cứu không còn chỉ là tìm công thức nghiệm mà chuyển sang các vấn đề cơ bản hơn: sự tồn tại, tính duy nhất và tính liên tục của nghiệm. Các kết quả của Cauchy và Picard đã đặt nền móng cho cách hiểu hiện đại về phương trình vi phân cấp một như một bài toán toán học chặt chẽ, vượt ra ngoài phạm vi tính toán thuần túy.

5. Kết luận
Lịch sử hình thành bài toán giải phương trình vi phân cấp một phản ánh rõ nét sự phát triển của toán học: từ nhu cầu mô tả chuyển động và biến thiên, qua các kỹ thuật tính toán, đến việc xây dựng một lý thuyết trừu tượng và nghiêm ngặt. Chính từ nền tảng này, lý thuyết phương trình vi phân đã phát triển mạnh mẽ và trở thành công cụ không thể thiếu trong khoa học và kỹ thuật hiện đại.