Chúng tôi giới thiệu khái niệm trường độ dốc thông qua một ví dụ. Xét phương trình vi phân cấp một

dy/dx = 0.2y                           (2)

Một hàm f là nghiệm của phương trình (2) nếu y = f(x) thỏa mãn phương trình (2) với mọi giá trị của x thuộc miền xác định của f. Diễn tả bằng hình học, phương trình (2) cho chúng ta biết độ dốc của đường cong đi qua điểm (x, y). Ví dụ, nếu y =f(x) là một nghiệm của phương trình (2) và đi qua điểm (0, 2), thì độ dốc của f tại (0,2) được cho bằng

dy/dx = 0.2(2) = 0.4

Chúng tôi minh họa mối quan hệ này bằng cách vẽ các đoạn thẳng ngắn của đường tiếp tuyến tại điểm (0, 2), như trong Hình 1A. Quy trình được lặp lại cho các điểm (-3, 1) và (2, 3). Giả sử đồ thị của f đi qua cả 3 điểm, ta vẽ một đồ thị gần đúng của f trong Hình 1B.

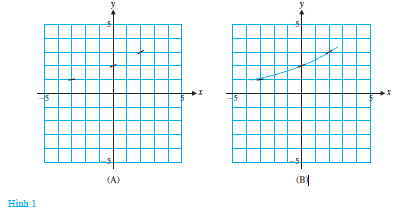
Nếu ta tiếp tục quá trình vẽ các đoạn tiếp tuyến tại các điểm trên lưới Hình 1—một việc dễ xử lí bằng máy tính, chứ không tính tay—ta có được trường độ dốc. Một trường độ dốc cho phương trình (2), được vẽ bằng máy tính, được cho trong Hình 2. Tổng quát, một trường độ dốc cho một phương trình vi phân cấp một thu được bằng cách vẽ những đoạn tiếp tuyến được xác định bởi phương trình tại mỗi điểm trên lưới tọa độ.