Cho P là số tiền ban đầu gửi vào một tài khoản, và cho A là số tiền trong tài khoản

tại thời điểm t bất kì. Thay vì giả định số tiền trong tài khoản sinh lãi với lãi suất cố

định, ta giả sử rằng tốc độ tăng của số tiền trong tài khoản tại thời điểm t bất kì là tỉ

lệ thuận với số tiền hiện có ở thời điểm đó. Vì dA/dt là tốc độ tăng của A theo t, ta có

dA/dt = rA           A(0) = P               A, P > 0           (1)

với r là một hằng số thích hợp. Ta muốn tìm một hàm số A = A(t) thỏa mãn các điều

kiện trên. Nhân cả hai vế của phương trình (1) với 1/A ta được

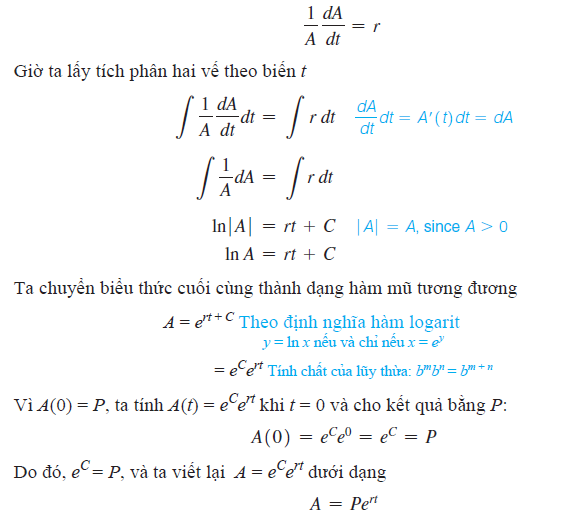
Công thức này giống công thức lãi kép liên tục thu được tại bài Hàm mũ, khi đầu tư số tiền gốc P với lãi suất kép liên tục hằng năm là r trong t năm.