Ứng dụng của toán trong khoa học tên lửa
Nhiều tên lửa như là Pegasus XL hiện được sử dụng để phóng các vệ tinh và Saturn V lần đầu tiên đưa con người lên mặt trăng, được thiết kế sử dụng ba tầng trong quá trình phóng lên không gian Tầng lớn đầu tiên bắt đầu đẩy tên lửa cho đến khi nhiên liệu của nó cạn kiệt, đến lúc này tầng đó được vứt bỏ để giảm khối lượng của tên lửa. Tầng thứ hai và tầng thứ ba nhỏ hơn có chức năng tương tự đưa trọng tải của tên lửa vào quỹ đạo quanh trái đất. (Với thiết kế này, cần ít nhất hai tầng để đạt được vận tốc cần thiết và việc sử dụng tên lửa ba tầng được chứng tỏ là sự cân bằng tốt giữa chi phí và hiệu năng.) Ở đây mục tiêu của chúng ta là xác định khối lượng của mỗi tầng trong ba tầng tên lửa sao cho giảm thiểu tổng khối lượng của tên lửa mà vẫn đảm bảo đạt được vận tốc mong muốn.
Đối với tên lửa một tầng tiêu thụ nhiên liệu với tốc độ không đổi, sự thay đổi vận tốc dẫn đến gia tốc của tên lửa được mô hình hóa bởi công thức
trong đó Mr là khối lượng của động cơ tên lửa kể cả nhiên liệu ban đầu, P là khối lượng của trọng tải, S là hệ số cấu trúc được quyết định bởi thiết kế của tên lửa (cụ thể, nó là tỷ lệ của khối lượng tên lửa không nhiên liệu trên tổng khối lượng của tên lửa với trọng tải), và c là vận tốc (không đổi) của khí xả so với tên lửa.
Bây giờ xem xét một tên lửa ba tầng và trọng tải có khối lượng A. Giả sử lực từ bên ngoài là không đáng kể và c và S không đổi với mỗi giai đoạn. Nếu Mi là khối lượng của tầng thứ i, thì ban đầu chúng ta có thể xem động cơ tên lửa có khối lượng M1 và trọng tải của nó có khối lượng M2 + M3 + A; tầng thứ hai và tầng thứ ba có thể được xử lý tương tự.
Qúa trình thực hiện bài toán (dự án)

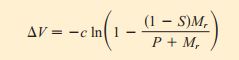
.JPG)
.JPG)

