Khi chúng ta biết được tốc độ thay đổi của một đại lượng (tức là biết đạo hàm của đại lượng đó) và giá trị ban đầu của đại lượng đó thì chúng ta có thể tìm được đại lượng đó bằng tích phân bất định. Từ đó chúng ta có thể dự đoán giá trị của nó trong tương lai. Để hiểu rõ hơn bản chất của quá trình này, chúng ta cùng xét mô hình sau đây: 

   Lợi nhuận cận biên của một cửa hàng bán xe khi bán được x chiếc xe mỗi tuần được cho bởi P'(x) = 4x + 10, trong đó P(x) là lợi nhuận thu được  tính bằng đô la. Lợi nhuận của cửa hàng khi bán được 20 chiếc xe mỗi tuần là 3,000 đô. Tìm hàm lợi nhuận và số lượng xe cần bán (làm tròn đến phần nguyên) để thu được lợi nhuận 12,000 đô mỗi tuần. Cửa hàng sẽ nhận được lợi nhuận bao nhiêu (làm tròn đến đơn vị đô la) nếu tuần đó bán được 70 chiếc xe ? 

   Theo mô hình trên, chúng ta đã biết được P'(x) , để tìm hàm P(x) ta chỉ cần lấy tích phân bất định của hàm P'(x) và thay điều kiện P(20) =3,000 ta sẽ có được hàm lợi nhuận P(x). Từ đó ta có thể dự đoán được lợi nhuận của cửa hàng khi bán 70 chiếc xe mỗi tuần.

   Ta có: Hàm lợi nhuận khi bán x chiếc xe là: 

                

  Lại có: 

             

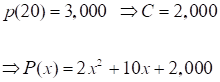
  Để lợi nhuận 12,0000 $ thì số xe cần bán ra là: P(x) = 12,000  => x = 68 (xe)