Ứng dụng của nguyên hàm trong bài toán lập hàm
Giả thiết của bài toán lập hàm gồm 2 yếu tố:
Giả thiết 1: xác định tốc độ thay đổi f’(x). Tính nguyên hàm của f’(x) để tìm f(x) (dạng tổng quát)
Giả thiết 2: xác định giá trị f(xo) = yo. Thay xo, yo vào hàm số f(x) tìm được ở bước trên để tìm hằng số.
Ta kết luận được công thức hàm f(x) cần tìm.
Bài toán 1: Nếu chi phí cận biên của việc sản xuất x đvsp được cho bởi công thức:
C’(x) = 0.3x2 + 2x (đvtt/đvsp).
Chi phí cố định là 2000 đvtt, hãy xác định hàm chi phí C(x) và chi phí sản xuất 20 đvsp.
Từ đề bài, ta có cặp giả thiết sau:
C’(x) = 0.3x2 + 2x và C(0) = 2000. Ta có:
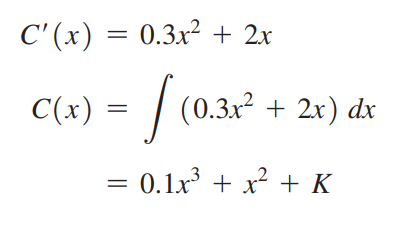
và 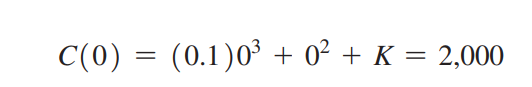
Vậy, hàm chi phí cần tìm là: C(x) = 0.1x3 + x2 + 2000
Chi phí sản xuất 20 đvsp là: C(20) = 3200 (đvtt).
Bài toán 2: Doanh số bán hàng của một cửa hàng sau t ngày đang thay đổi với tốc độ là S’(t) = 60t1/2 (đvsp/ngày).
Hiện tại, doanh số bán hàng đạt 27 000 đvsp. Xác định hàm doanh số S(t) và thời gian cần để doanh số bán hàng đạt 41000 đvsp.
Từ đề bài, ta có cặp giả thiết:
S’(t) = 60t1/2 và S(0) = 27000.
Ta có:

và
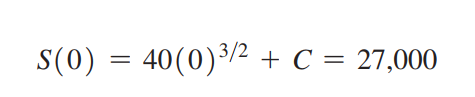
Do đó, S(t) = 40t3/2 + 27000 (đvsp).
Khi đó, để doanh số đạt 41000 đvsp thì
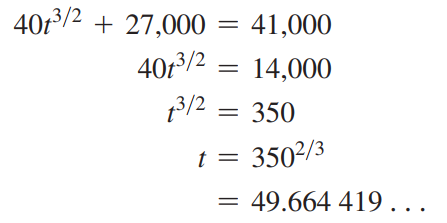
Vậy sau khoảng 50 ngày thì doanh số đạt 41000 đvsp.


