Chúng ta dùng một số kí hiệu sau: 

x là số đvsp được sản xuất và bán ra (đvsp), p là giá bán của một đvsp (đvtt), R là doanh thu thu được tương ứng khi bán ra x đvsp với giá bán p. Khi đó R = x.p.

Trong trường hợp bán nhiều đvsp thì ta sẽ có các giá bán tương ứng và doanh thu tương ứng của mỗi loại sản phẩm. Để thống kê số liệu cho từng sản phẩm, ta có thể sử dụng ma trận mô tả các dữ liệu đó.

Bài toán 1: Công ty ABC bán 3 loại sản phẩm là M1, M2, M3 với giá bán lần lượt là p1 = 15, p2 = 20, p3 = 35 (đvtt). Số lượng sản phẩm bán được tưng ứng lần lượt là x1 = 100, x2 = 120, x3 = 320. Ta có thể kí hiệu X là ma trận số đvsp, khi đó, ta có:

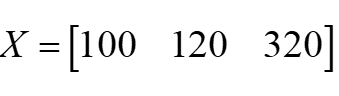
Kí hiệu P là ma trận giá bán:

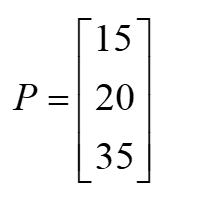
Khi đó, phép nhân hai ma trận X.P cho chúng ta ma trận doanh thu của công ty khi bán hết số lượng sản phẩm tương ứng, cụ thể:

Vậy doanh thu tương ứng là 15100 đvtt

Bài toán 2: Công ty ABC có 2 chi nhánh bán 3 loại sản phẩm như trên. Số lượng sản phẩm bán được của mỗi sản phẩm của chi nhánh 1, 2 lần lượt là 100,120, 320 (đvsp) - chi nhánh 1 và 250,75, 380 (đvsp) - chi nhánh 2.

Khi đó, ma trận số đvsp và ma trận giá bán là:

 

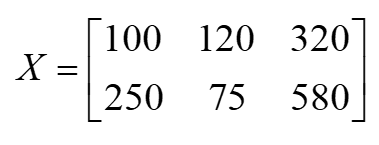
và

  

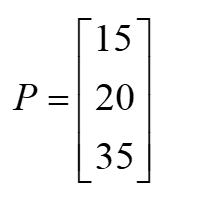
Ta dùng phép nhân ma trận X.P xác định được doanh thu của từng chi nhánh trong công ty.

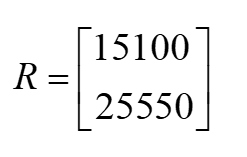
Khi đó, doanh thu của chi nhánh 1 là 15100 đvtt, doanh thu của chi nhánh 2 là 25550 đvtt.

Trong trường hợp số lượng sản phẩm và chi nhánh tăng lên thì phép nhân hai ma trận giúp chúng ta xác định được ma trận doanh thu - thể hiện doanh thu của từng chi nhánh.