Một công ty tư vấn cho một công ty sản xuất hàm thiết lập hàm sản xuất Cobb–Douglas cho một sản phẩm cụ thể như sau:

                                  N(x, y) = 50x^0.8y^0.2

Trong phương trình này, x là số đơn vị nhân công và y là số đơn vị vốn cần thiết để sản xuất N(x, y) đơn vị sản phẩm. Mỗi đơn vị nhân công tốn $40 chi phí, mỗi đơn vị vốn tốn $80 chi phí.

 Nếu $400 000 được đầu tư để sản xuất sản phẩm này, hãy xác định khoản tiền này nên được phân bổ như thế nào để tối đa hóa sản suất, và tìm mức sản xuất tối đa.

Giải: Điều kiện của bài toán là 40x + 80y = 400 000

Đặt g(x,y) = 40x + 80y

Sau đó tính các đạo hàm riêng của hàm và tìm điểm tới hạn.

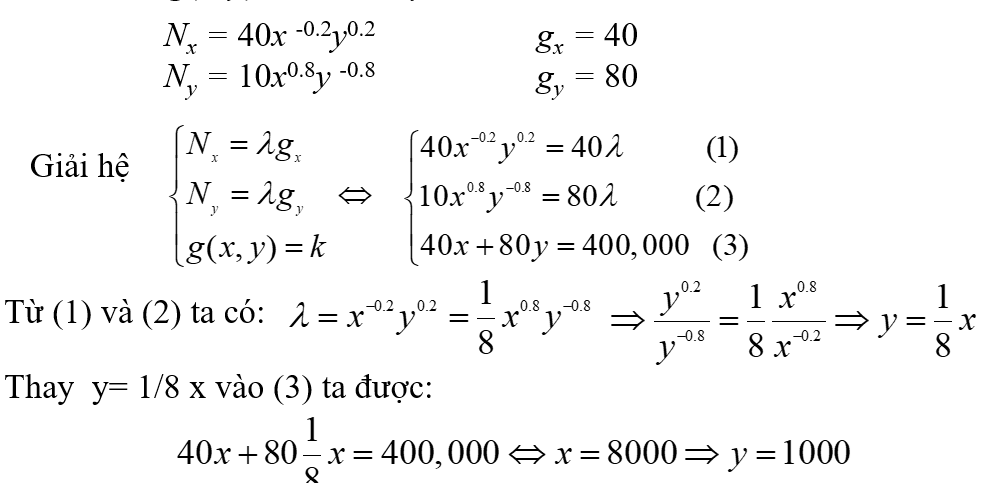
Vậy công ty nên phân bổ 8000 đôla vào nhân công và 1000 đôla vào đơn vị vốn thì mức sản xuất tối đa.

max N(x, y) = N(8000, 1000) =263901.6 đvsp