Vào năm 1990, dân số thế giới là 5.292 tỷ người và hàng năm dân số tăng với tốc độ không đổi khoảng 2%. Nếu mô hình tăng trưởng này sẽ tiếp tục, thì tốc độ tăng dân số được chỉ ra trong đường cong hình 1a. Đây là đồ thị của một hàm mũ, P(t) = b^t, trong đó b= 1.0202. Tỷ lệ thay đổi phần trăm của hàm dân số P(t) là không đổi (tức là, 2%), nhưng P(t) tăng một cách nhanh chóng theo thời gian, vào năm 2010, mô hình dự đoán dân số thế giới gần bằng 48 tỷ người.

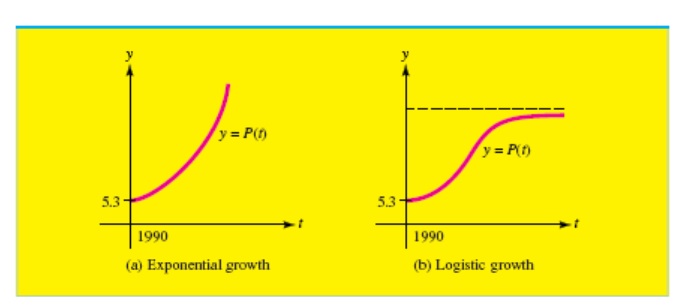
   Hình 1 Hai mô hình phát triển dân số

    Mô hình này đôi khi được gọi là mô hình phát triển dân số của Malthusian, sau Malthusian(1766 - 1834), một nhà kinh tế học người Anh đã sử dụng nó để hỗ trợ cho sự khẳng định của anh ta rằng dân số tăng nhanh hơn sự cung cấp thức ăn. May mắn, có giả thuyết của mô hình toán của Malthusiani. Đặc biệt, đồ thị trong hình 1b được dựa vào mô hình dân số được gọi là logictis, mà nó được giả sử rằng sự tăng trưởng dân số dần dần bị “phanh lại” bởi các điều kiện môi trường. Đường cong nào cung cấp cho bạn một bức tranh hiện thực hơn về sự tăng trưởng dân số thế giới?

          Sự phát triển Logistic có thể được mô tả bằng các số hạng của hàm mũ, và nó có thể có một số ứng dụng quan trọng khác. Chẳng hạn, hàm mũ được sử dụng trong nhân khẩu học để dự báo kích cỡ của dân số, trong tài chính thì dùng để tính giá trị của sự đầu tư, trong khảo cổ thì để ghi các ngày tháng của các vật cổ, trong tâm lý học dùng để nghiên cứu sự học của các người phi thường, và trong công nghiệp dùng để đánh giá sự tin cậy của các sản phẩm. Chúng ta sẽ nghiên cứu các tính chất của hàm mũ và giới thiệu một vài mô hình cơ bản trong một số hàm mà nó đóng một vai trò quan trọng. Bổ sung một số ứng dụng như mô hình logictis được khảo sát trong các phần tiếp theo.