Chúng ta đã biết cách tính vi phân của nhiều dạng hàm một biến độc lập và giải thích các kết quả đạo hàm. Vậy còn những hàm có hai hoặc nhiều biến độc lập thì thế nào? Chúng ta hãy quay trở lại ví dụ về ván lướt sóng ở bài trước.

Khi công ty chỉ sản xuất một loại ván tiêu chuẩn, thì hàm chi phí là

C(x) = 500 + 70x

Lấy vi phân theo x, ta có hàm chi phí biên

C’(x) = 70

Vì chi phí biên là hằng số, nên $70 là mức thay đổi chi phí khi tăng mức sản xuất thêm 1 đơn vị tại bất kỳ mức sản lượng nào.

Khi công ty sản xuất hai mẫu ván lướt-mẫu tiêu chuẩn và mẫu thi đấu, thì hàm chi phí là

C(x, y) = 700 + 70x + 100y

Bây giờ giả sử chúng ta lấy vi phân theo x, giữ y cố định và ký hiệu hàm kết quả là C_x(x, y); hoặc giả sử chúng ta lấy vi phân theo y, giữ x cố định, và ký hiệu hàm kết quả là C_y (x,y). Lấy vi phân theo cách này ta có

C_x(x, y)= 70             C_y(x, y) = 100

Từng hàm số này được gọi là đạo hàm riêng, và trong ví dụ này, mỗi hàm thể hiện chi phí cận biên. Hàm đầu tiên là mức thay đổi chi phí do tăng 1 đơn vị sản phẩm ván trượt tiêu chuẩn được sản xuất ra trong khi số lượng ván thi đấu không đổi. Hàm thứ hai là mức hay đổi chi phí khi tăng 1 đơn vị sản phẩm ván thi đấu trong khi mức sản xuất ván tiêu chuẩn không đổi.

Nhìn chung, nếu z = f (x, y), thì đạo hàm riêng của f theo x, ký hiệu ∂z/∂x, f_x hoặc f_x(x, y), được xác định bằng

                 

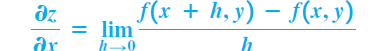
nếu giới hạn này tồn tại.

Tương tự đạo hàm riêng của f theo y, ký hiệu ∂z/∂y, f_y hoặc f_y(x, y), được xác định bằng :

                

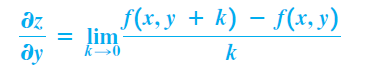
đây là đạo hàm riêng của f theo y, xem x là hằng số.