Chúng ta có thể sử dụng máy tính để giải quyết những bài toán tối ưu—bài toán về tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của một hàm số. Như nội dung đã trình bày trong mục, lưu ý rằng yêu cầu của bài toán không phải lúc nào cũng là tối ưu hàm số đã có sẵn. Thông thường, ta phải tự tìm ra hàm số và sau đó tìm cực trị tuyệt đối thích hợp.

Các phương pháp được sử dụng để giải quyết các bài toán tối ưu được minh họa qua ví dụ sau.

Một chủ nhà sư dụng $320 để xây một hàng rào quanh khu vườn hình chữ nhật. Ba mặt của hàng rào sẽ được rào bằng hàng rào thép với giá $2/m. Mặt còn lại được rào bằng hàng rào gỗ với giá $6/m. Tìm các kích thước và diện tích lớn nhất của khu vườn sao cho chi phí cần sử dụng là $320.

Giải: Trước hết, ta nên vẽ hình (Hình1 ), giới thiệu các biến, xác định mối quan hệ giữa các biến.

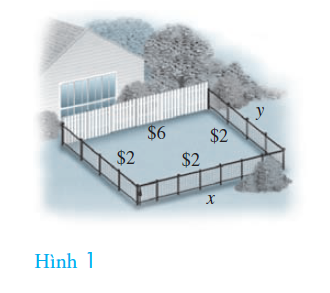
Do ta chưa biết các kích thước của khu vườn nên chiều dài của hàng rào được biểu diễn bằng biến x và y. Chi phí của vật liệu hàng rào đã cố định là một hằng số.

Tiếp theo, ta xác định mối quan hệ giữa các biến . Diện tích của khu vườn là

                                     A = xy

và chi phí của hàng rào là:

                                 C = 2y + 2x + 2y + 6x

                                    = 8x + 4y

Vấn đề đặt ra là chủ nhà chỉ có $320 để sử dụng. Giả sử rằng diện tích lớn nhất xảy ra khi sử dụng hết số tiền được cho. Bài toán trở thành

                      Cực đại A = xy thỏa mãn 8x + 4y = 320

Trước khi sử dụng máy tính để tìm diện tích lớn nhất A, ta phải biểu diễn A thành hàm số theo một biến. Ta sử dụng phương trình chi phí để rút biến y theo x, ta được biểu thức diện tích mới (tương tự, có thể rút x theo y).

                        8x + 4y = 320

                                4y = 320 - 8x

                                  y = 80 - 2x

                     A = xy = x(80 - 2x)= 80x - 2x²

Xét hàm số theo biến x. Vì x là một kích thước của hình chữ nhật nên điều kiện của x là