BÀI TOÁN QUY LUẬT TĂNG TRƯỞNG SUY TÀN
BÀI TOÁN QUY LUẬT TĂNG TRƯỞNG SUY TÀN
Mô hình tăng trưởng tự nhiên dP/dt = kP và mô hình theo phương trình Logistic dP/dt = kp(1 – P/M) là hai mô hình toán về quy luật tăng trưởng của một quần thể. Tuy nhiên trong thực tế, nhiều trường hợp sự tăng trưởng và suy tàn của quần thể được mô phỏng bởi các phương trình vi phân khác, gần giống với phương trình Logistic.
- Mô hình 1: Tăng trưởng - thu hoạch: Ví dụ một quần thể cá được nuôi trong một hồ có sức chứa M, tốc độ thu hoạch là một số không đổi c. Khi đó thay vì tốc độ tăng trưởng tuân theo quy luật phương trình Logistic, nó được tính như sau:
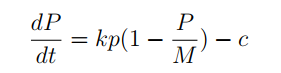
Từ mô hình này, người nuôi có thể đề xuất các phương án về số lượng nuôi ban đầu, quy mô lượng nuôi, khai thác... sao cho phù hợp.
- Mô hình 2: Tuyệt chủng: Với nhiều loài, khi số lượng cá thể xuống dưới mức tối thiểu m nào đó vì dịch bệnh, thiên tai, bị khai khác..., chúng dần đi đến sự tuyệt chủng. Lúc đó sự suy giảm cá thể được mô hình hóa bởi phương trình vi phân sau:
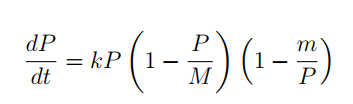
Mô hình này giúp các nhà bảo tồn có phương án can thiệp thích hợp, ngăn chặn sự tuyệt chủng của các loài quý hiếm trong tự nhiên.
- Mô hình 3: Tăng trưởng và suy tàn theo mùa: Trong tự nhiên, nhiều loài động, thực vật sinh sản, phát triển theo mùa thích hợp trong năm. Khi đó, sự tăng giảm số cá thể được mô hình hóa bởi phương trình vi phân sau:
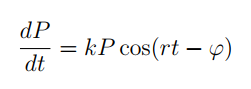
với k, r, ϕ là các hằng số dương. Mô hình này giúp đề xuất các phương án phòng trừ, diệt các loài có hại ... đạt hiệu quả, đúng thời điểm.
- Mô hình loài săn mồi - con mồi và sự cân bằng sinh thái: Trong tự nhiên, sự tăng hay giảm của loài săn mồi ảnh hưởng đến số lượng của con mồi và ngược lại. Do đó sự tăng giảm của các cặp loài như vậy được biểu diễn bởi một hệ các phương trình vi phân. Số lượng của cả hai loài đạt ở mức ổn định thì gọi là nghiệm cân bằng, gọi là sự cân bằng sinh thái.
Tài liệu tham khảo: Giải tích Calculus 7e (tập 1) – tác giả: James Stewart


