Một vấn đề lớn liên quan đến kinh tế học và xã hội học đó là phân bố sự giàu có trong xã hội. Một công cụ để đo tính không đồng đều trong phân bố sự giàu có là đường cong Lorentz, nó cung cấp cho ta một thông tin khá nhanh, và điều này được minh họa bởi phần trăm mà xã hội nhận với phần trăm sự giàu có của xã hội.

     Một loại đường cong Lorentz y =L(x)  được chỉ ra trong hình 6.20, trong đó hàm L(x) tỷ lệ thu nhập hàng năm mà quốc gia nhận thấp nhất là 100x% của dân số với 0 ≤ x ≤ 1 . Chẳng hạn, điểm (0.3; 0.23) trên đường cong biểu diễn các gia đình có thu nhập thấp là 30% chiếm 23% tổng thu nhập quốc dân.

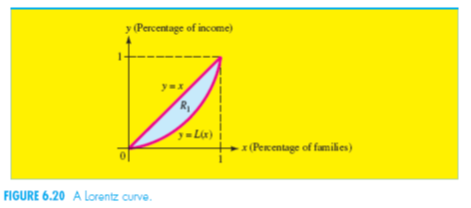
Đường thẳng y = x  diễn tả ý tưởng tương ứng với việc bằng nhau hoàn toàn trong phân bố của thu nhập (một gia đình có thu nhập thấp 100r% sẽ nhận 100r%  sự giàu có của quốc dân). Vì ý tưởng này không bao giờ nhận được trong thực tế, thường thì đường cong Lorentz nằm dưới đường thẳng y = x, như được chỉ ra trong hình 6.20. Diện tích của miền tô đậm R_1­ giữa đường thẳng y = x và đường cong Lorentz biểu diễn độ lệch của phân bố thực tế từ việc bằng nhau hoàn toàn, và tỷ số diện tích này là tổng diện tích của miền R_2­ dưới đường thẳng y = x trên 0 ≤ x ≤ 1 cung cấp phạm vi không bằng nhau trong phân bố sự giàu đã biểu diễn bởi đường cong. Vì miền tam giác R₂ có diện tích (1/2).(1).(1)=1/2  , tỷ số này được gọi là chỉ số Gini (chỉ số của thu nhập không đồng nhau), có thể được tính bằng công thức 

Chỉ số Gini luôn nằm giữa 0 và 1. Chỉ số 0 tương ứng với phân bố hoàn toàn cân bằng, và chỉ số 1 tương ứng với phân bố hoàn toàn không cân bằng (một gia đình có tất cả thu nhập). Chỉ số nhỏ hơn, sự phân bố giàu sẽ cân bằng hơn , và chỉ số lớn hơn, sự giàu chỉ được tập trung ở một vài bộ phận.